4 Basic plotting

Simple scatter plots

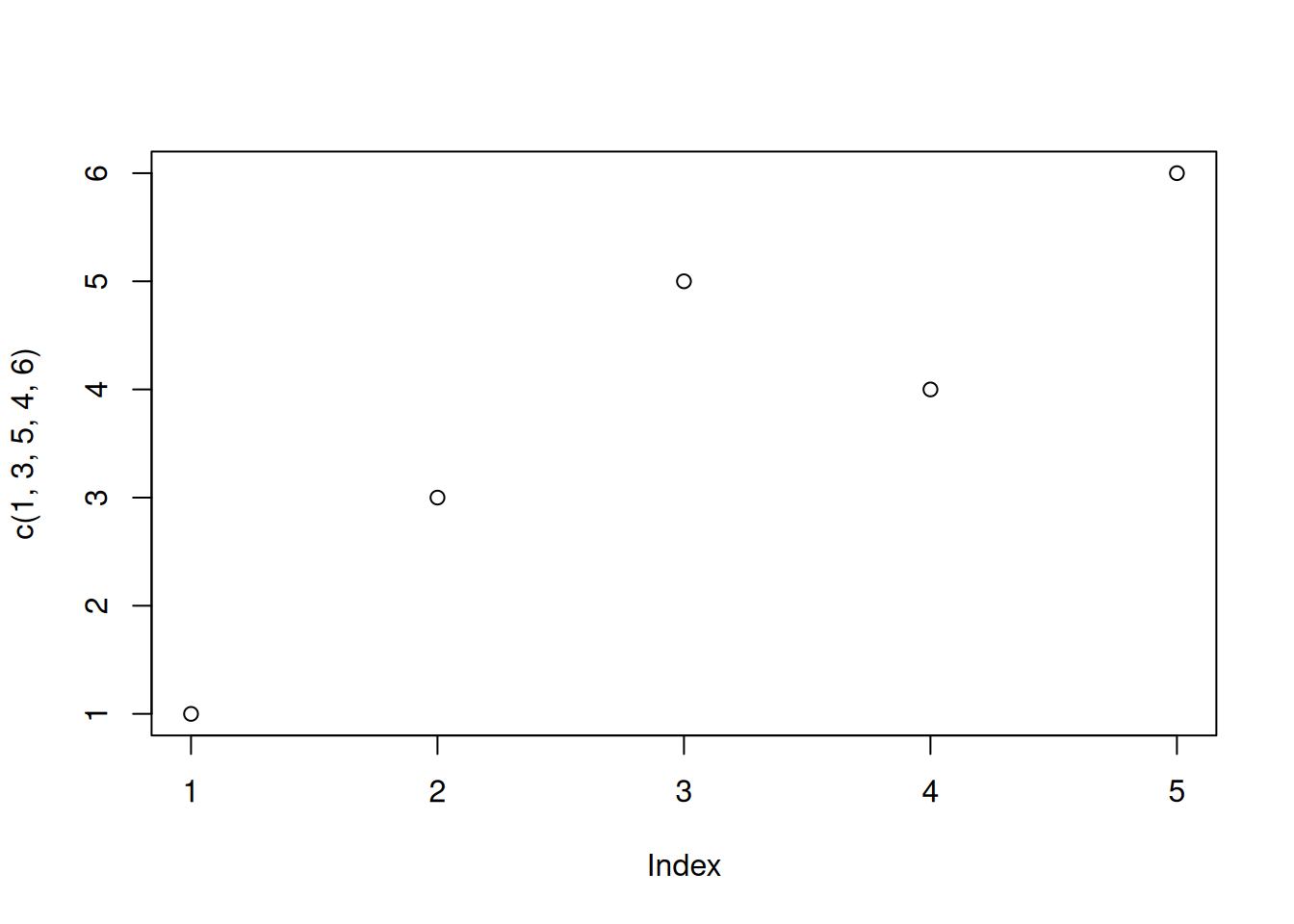
Scatter plots and line plots are created with the plot command. (Use help(plot) for detailed description.)
Simplest use: plot(y) or plot(x,y).

plot(c(1,3,5,4,6))

A plot with separate x and y coordinate vectors

my_x_values <- c(-2, -1.5, 0, 1.7, 2.3)
my_y_values <-  c(1,3,5,4,6)
plot(my_x_values, my_y_values)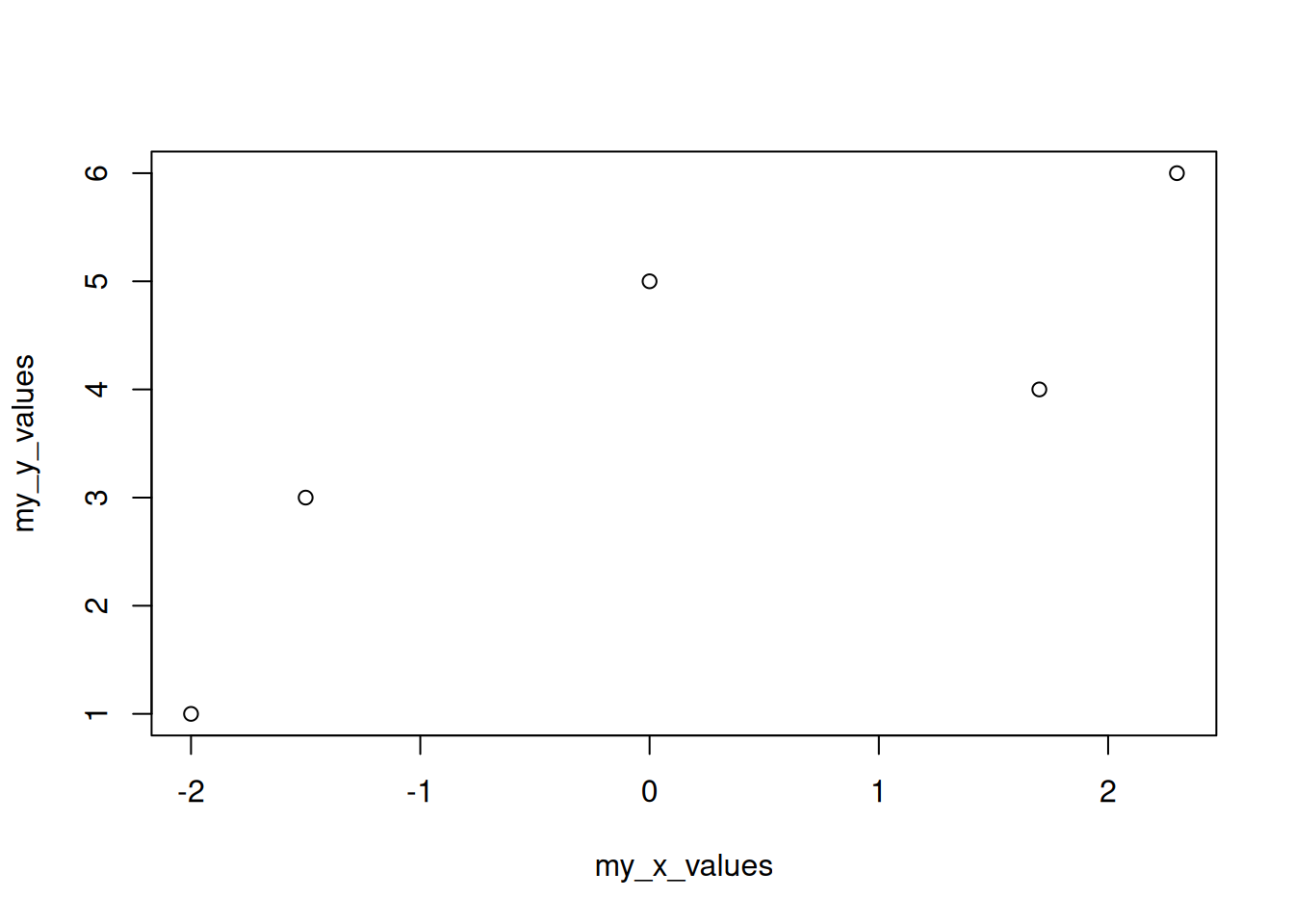

Plotting a mathematical expression

x <- -5:5
y <- x^2
plot(x, y)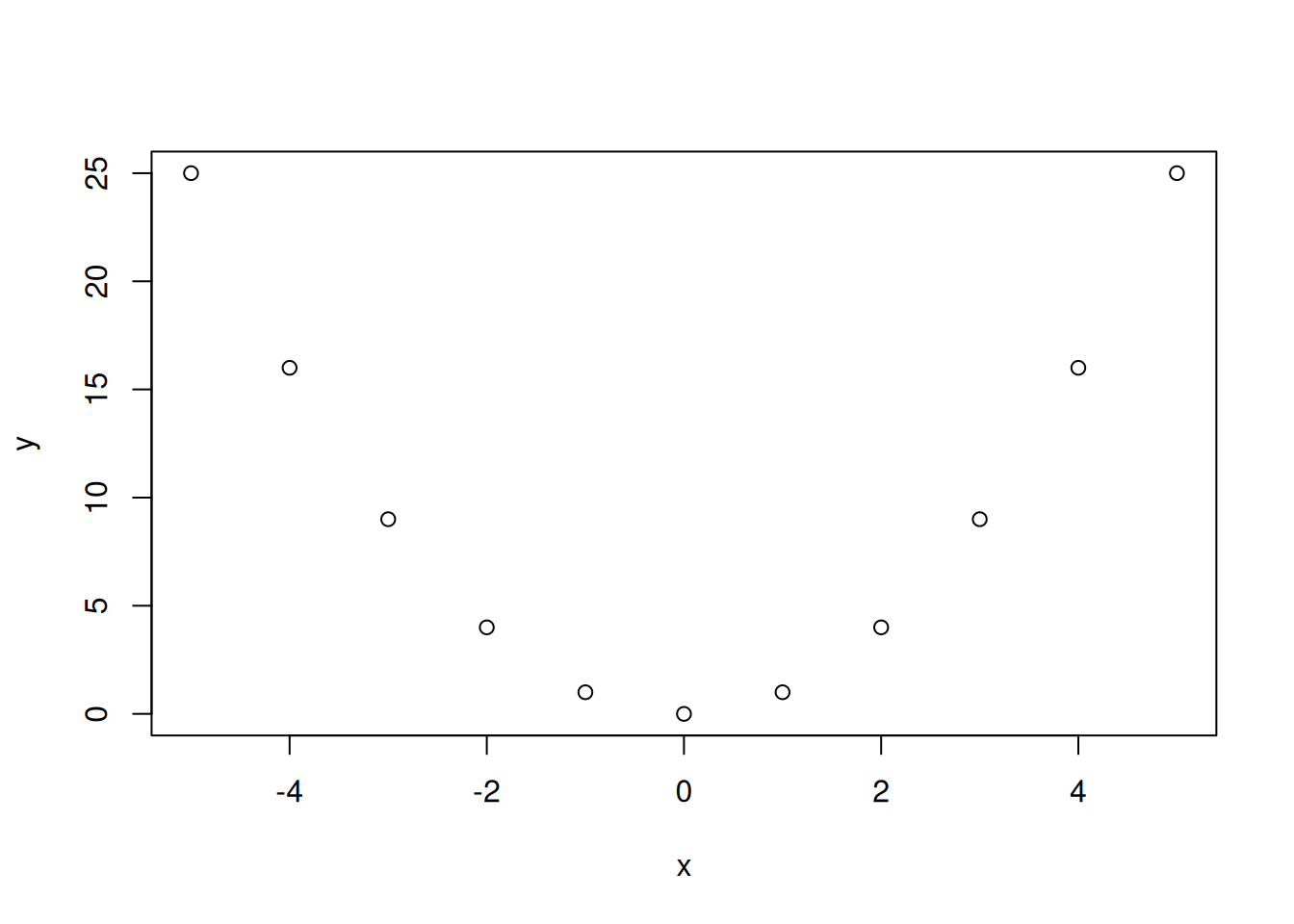

Change the axis labels and the title

heights <- c(1.70, 1.67, 1.75, 1.62, 1.81)
weights <- c(65, 70, 66, 61, 85)
plot(heights, weights, xlab="height (m)", ylab="weight (kg)")
title("Weight vs. height")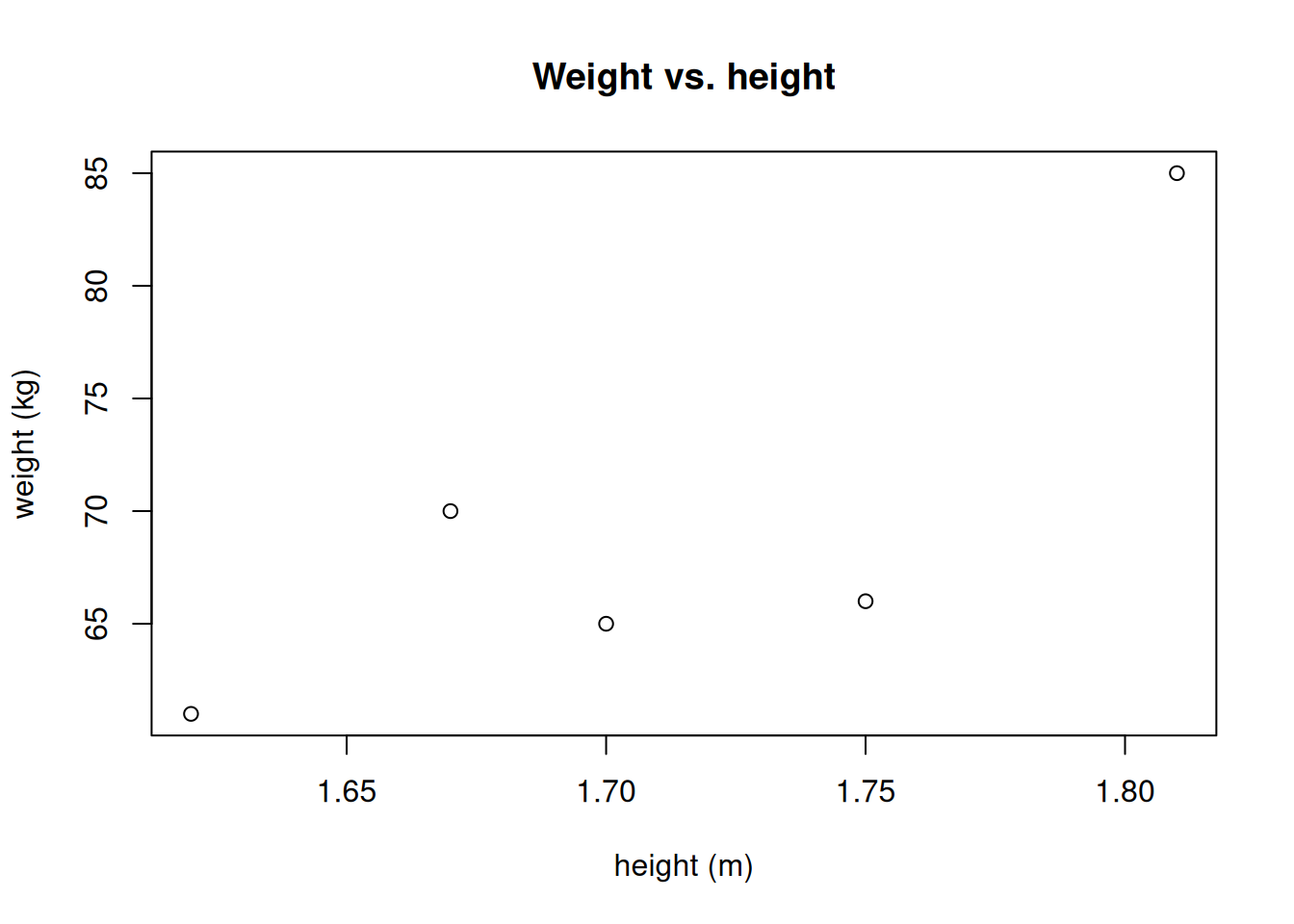

Change the marker shape and color

plot(heights, weights, pch=4, col="red", xlab="height (m)", ylab="weight (kg)")
title("Weight vs. height")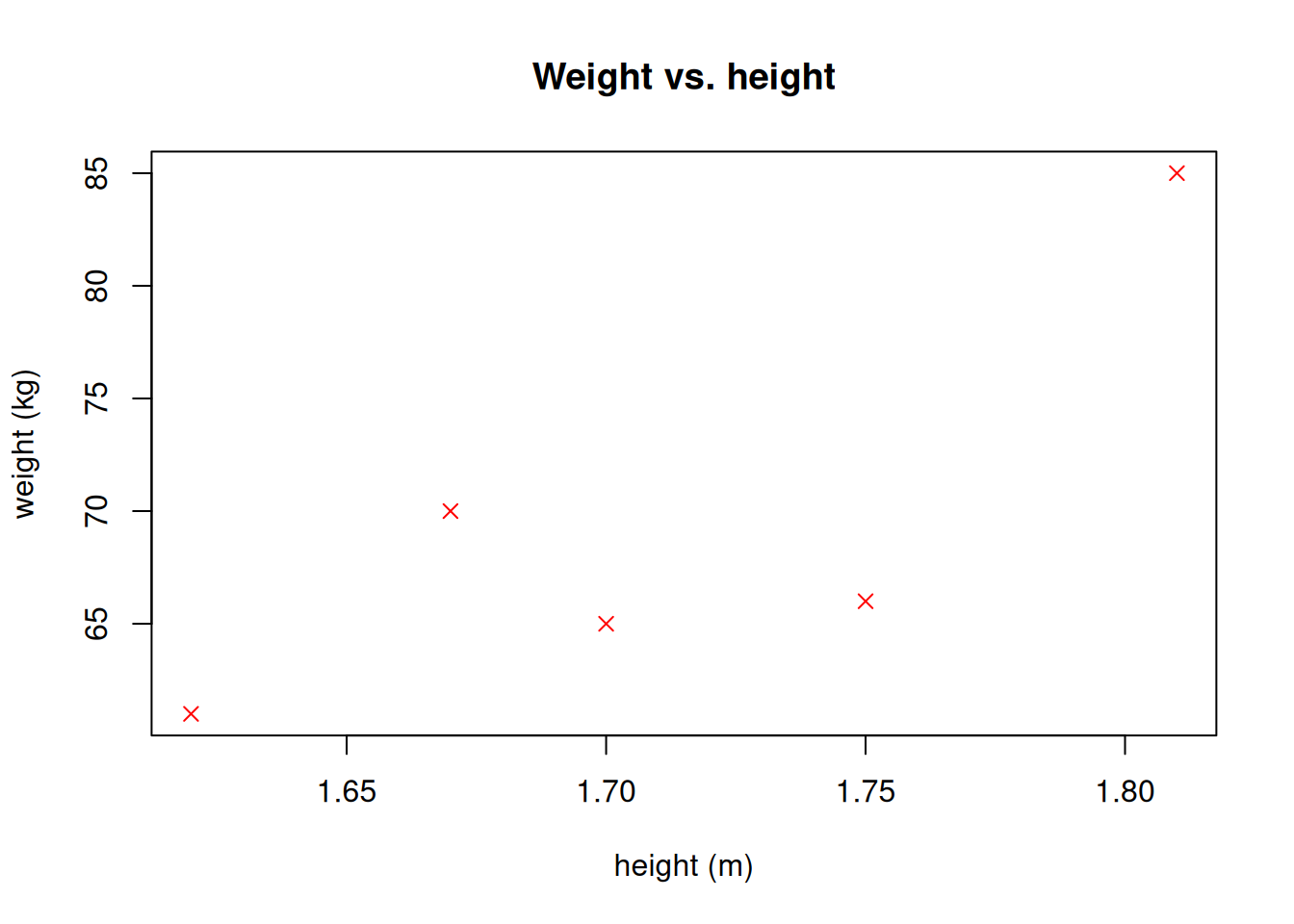

For details of setting the marker shape, size, and color see this document: https://www.statmethods.net/advgraphs/parameters.html

Exercise

Given the variables

x <- -5:5
y <- 1 - x^2 / 25

generate the following plot.

Line plots

x <- -5:5
y <- x^2
plot(x,y,type="l")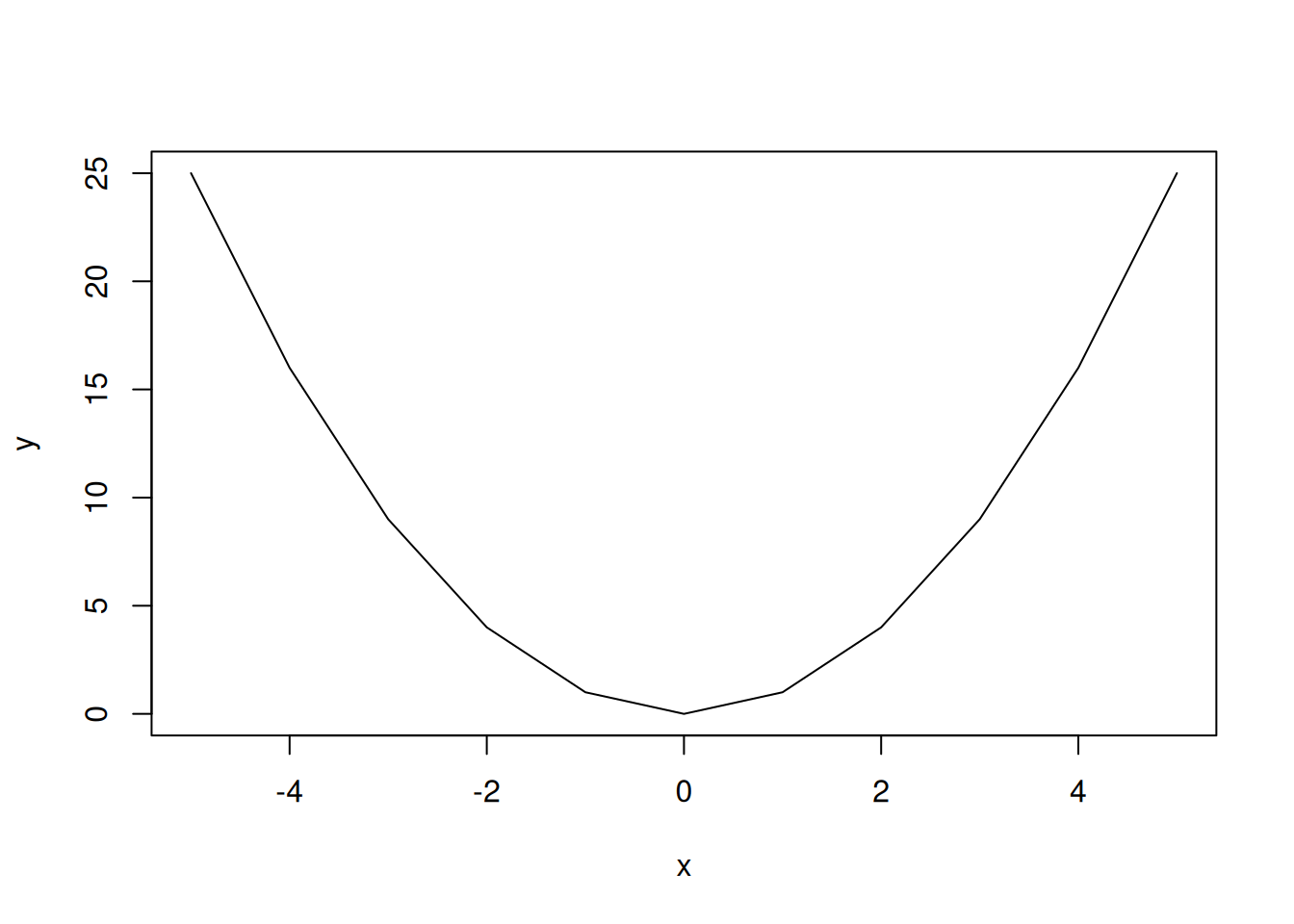

Suppose we plot the weights of people against their heights:

heights <- c(1.70, 1.67, 1.75, 1.62, 1.81)
weights <- c(65, 70, 66, 61, 85)
plot(heights, weights, type="l")

Since the data is not ordered, the line plot is zigzagging around. In this particular case, ordering weights with respect to heights produces a more pleasing plot.

plot(sort(heights), weights[order(heights)], type="l")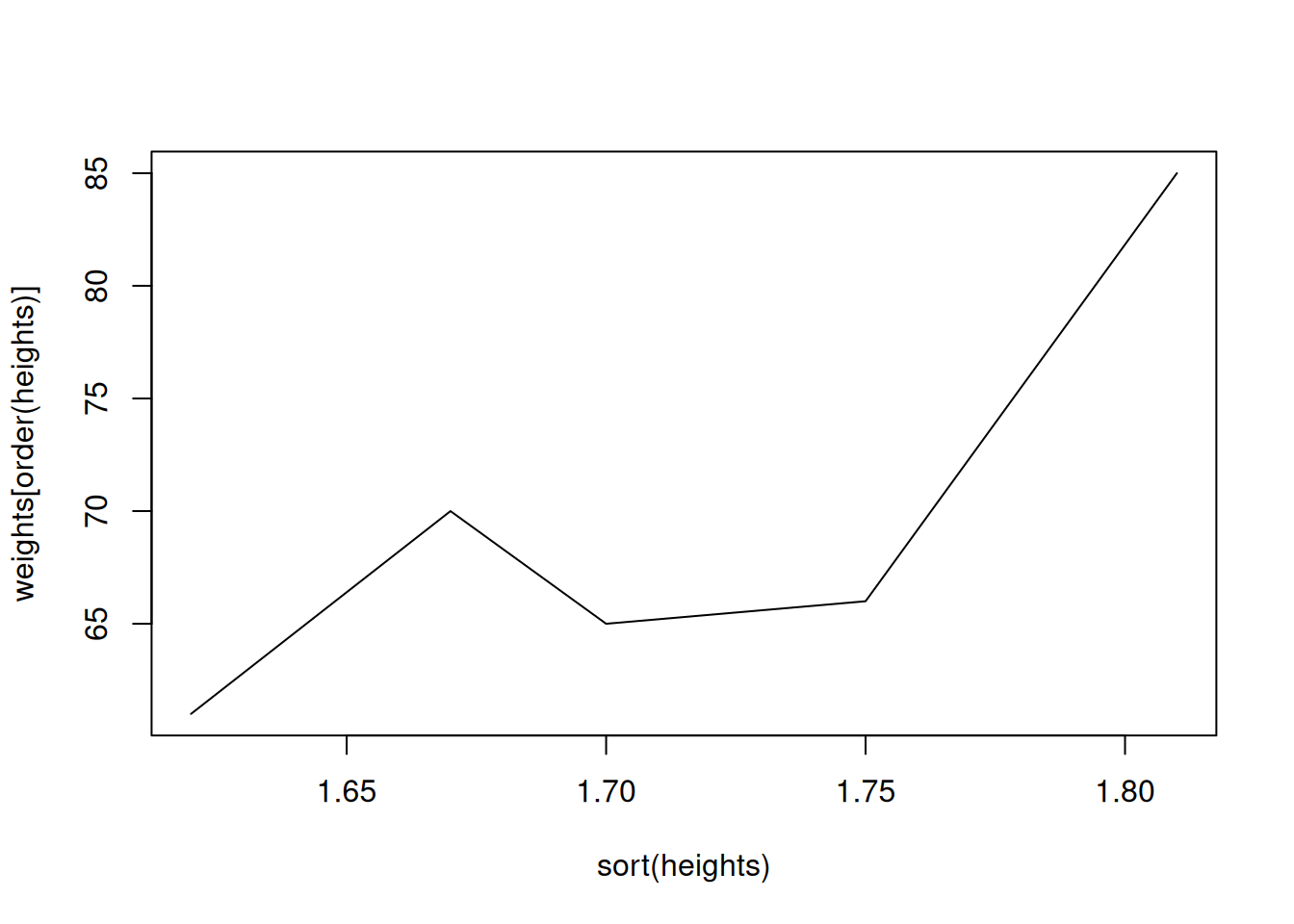

Function plotting

Plot the function \(y(x) = \mathrm{e}^{-0.1x^2}\sin(x)\).

x <- seq(-10, 10, length.out = 201)
y <- exp(-0.1*x^2)*sin(x)
plot(x, y, type="l", col="darkgreen")
title("A function")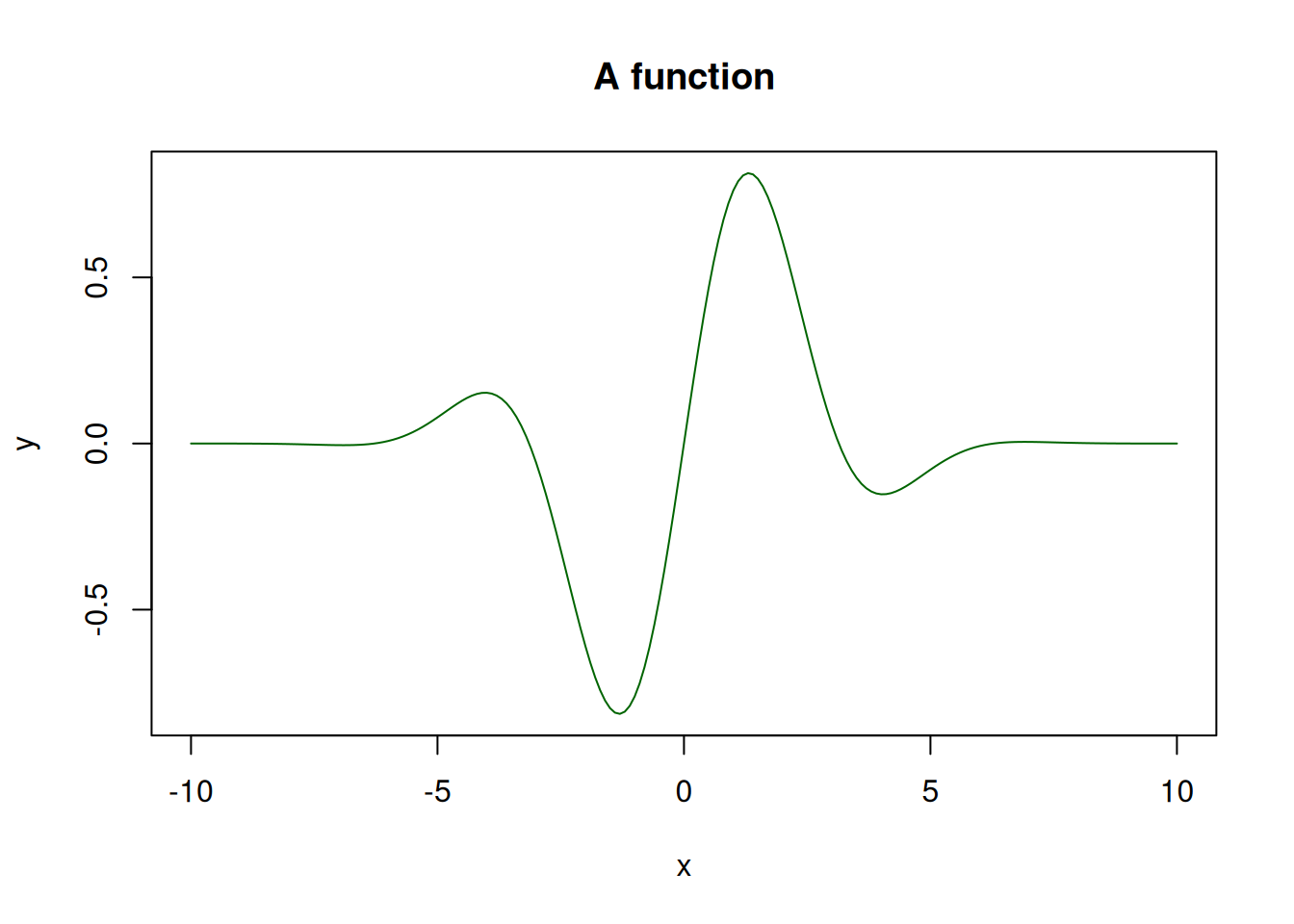

Plotting two functions together

Plot the functions \(y_1(x) = \mathrm{e}^{-0.1x^2}\sin(x)\) and \(y_2(x) = \sin(x)\) on the same graph.

x <- seq(-10,10, length.out = 101)
y1 <- exp(-0.1*x^2)*sin(x)
y2 <- sin(x)
plot(x, y1, type="l", col="red")
points(x, y2, type="l", col="blue")
title("Two functions")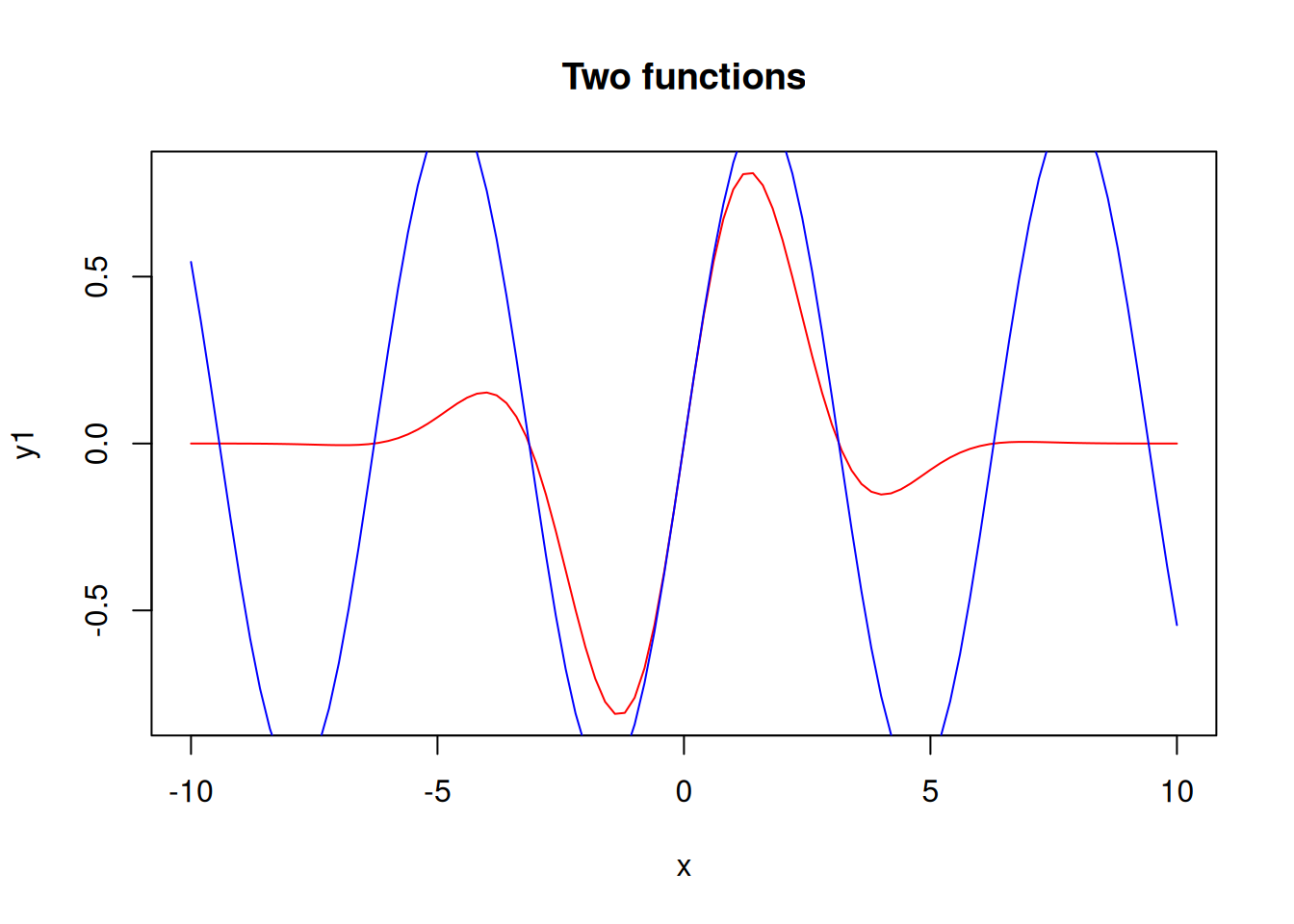

The y-axis limits are set according to the first plot, so the second plot appears cropped. To fix this, let’s set the limits manually.

plot(x, y1, ylim=c(-1.1, 1.1), type="l", col="red")
points(x, y2, type="l", col="blue")
title("Two functions")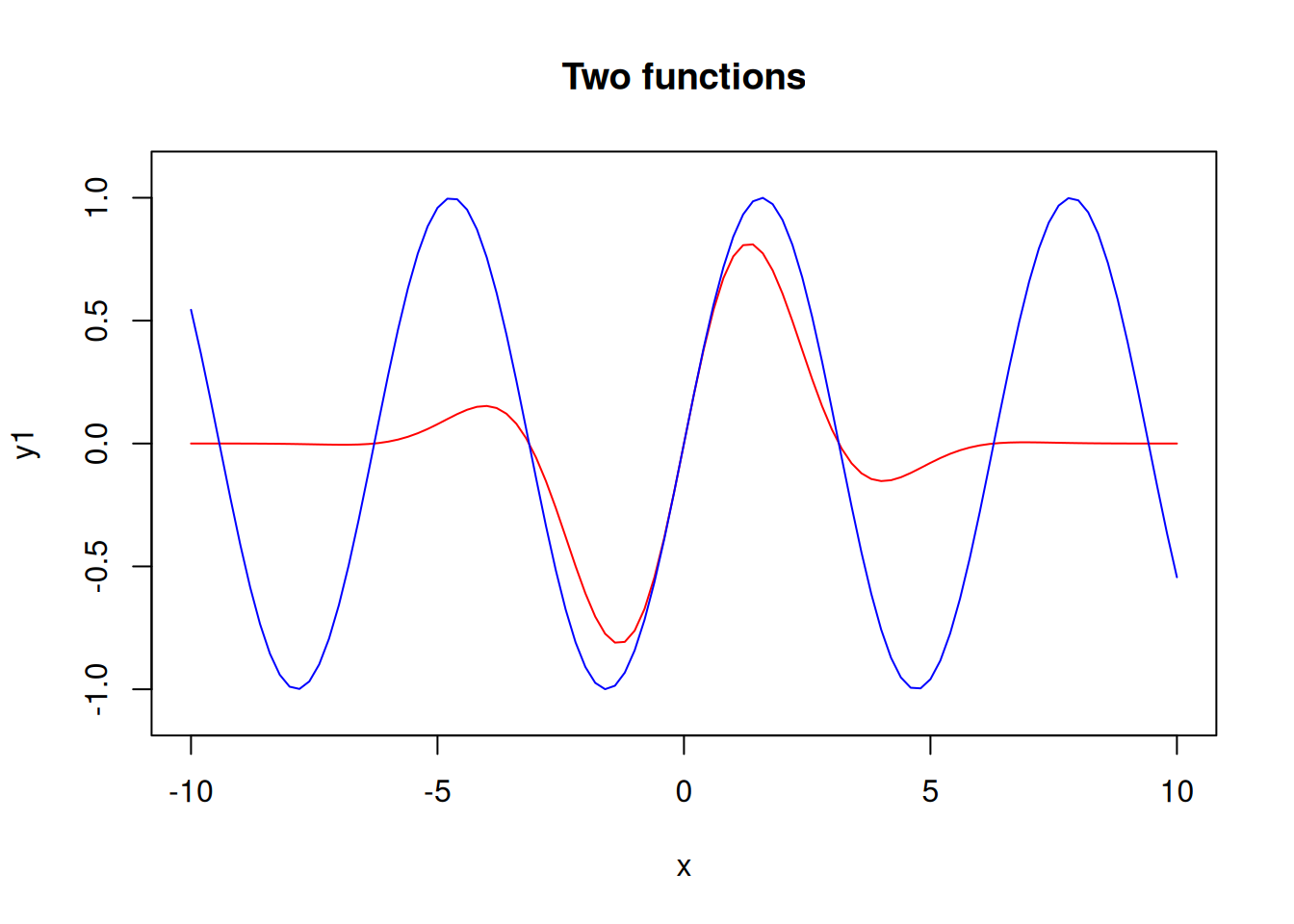

Exercise

The Taylor expansion of a function is a polynomial approximation to that function around a chosen point. For example, the Taylor expansion to \(\sin(x)\) around \(x=0\) is the infinite series: \[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\].

When we stop the terms at some points, the resulting polynomial becomes an approximation to \(\sin(x)\) around \(x=0\). For example, if we use only the first term, our approximation is: \[\sin(x)\approx x\] If we use the first two terms, the approximation has less error: \[\sin(x)\approx x - \frac{x^3}{3!}\] etc.

Plot the sine function from \(x=-4\) to \(x=4\) in red, and then plot each approximation, up to four terms, on the same frame. Observe how the subsequent polynomials converge to the sine function.

Histograms

A histogram divides the range of the data into “bins”, displays the count of points in each bin.

x <- c(rep(17,4), rep(18,7), rep(19,5), rep(20,5), rep(21,4))  
# Remember that rep(17,4) gives (17,17,17,17)
x

 [1] 17 17 17 17 18 18 18 18 18 18 18 19 19 19 19 19 20 20 20 20 20 21 21 21 21

hist(x, col="blue")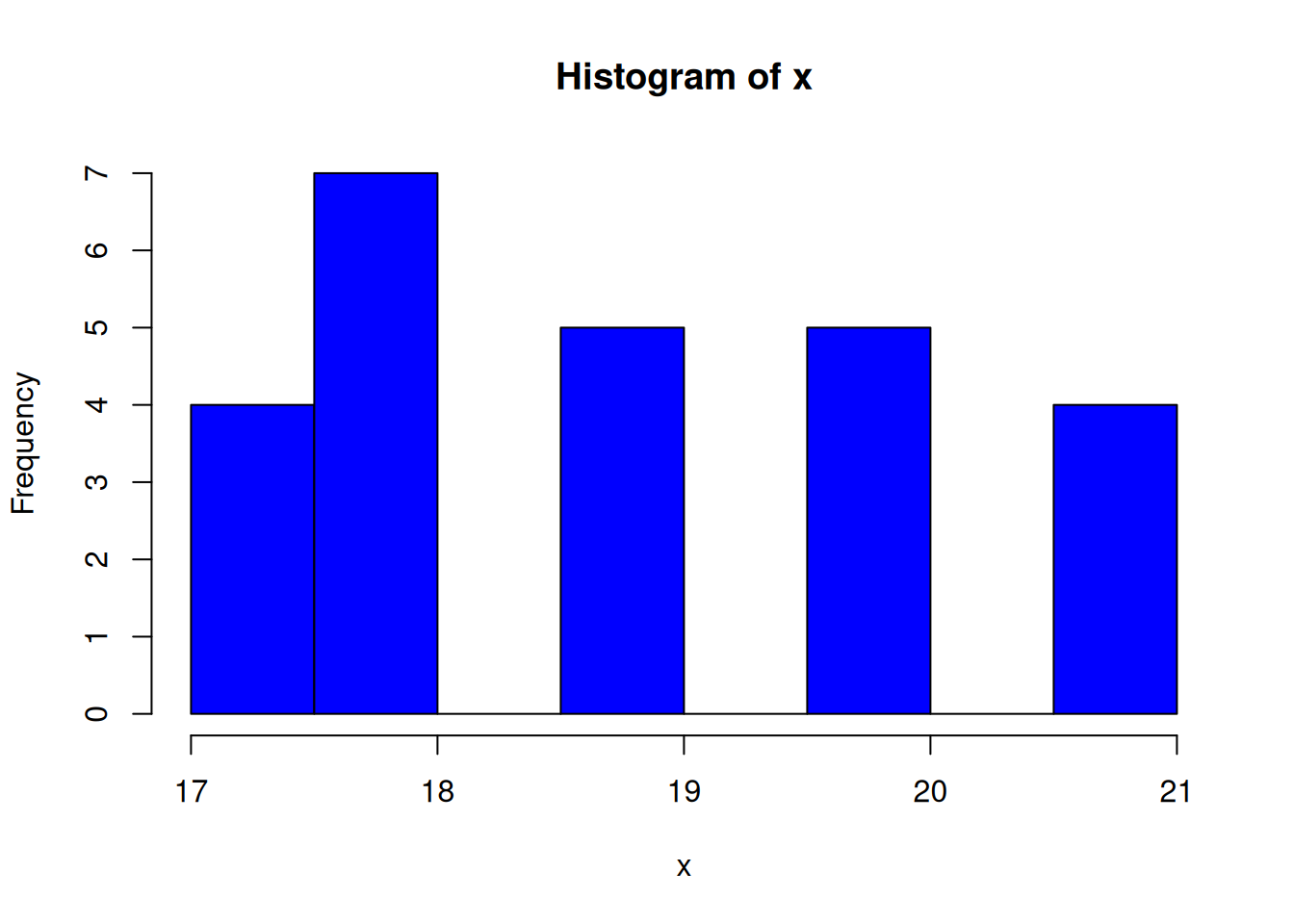

Specify the break points of the histogram:

hist(x, col="red", breaks=15:22)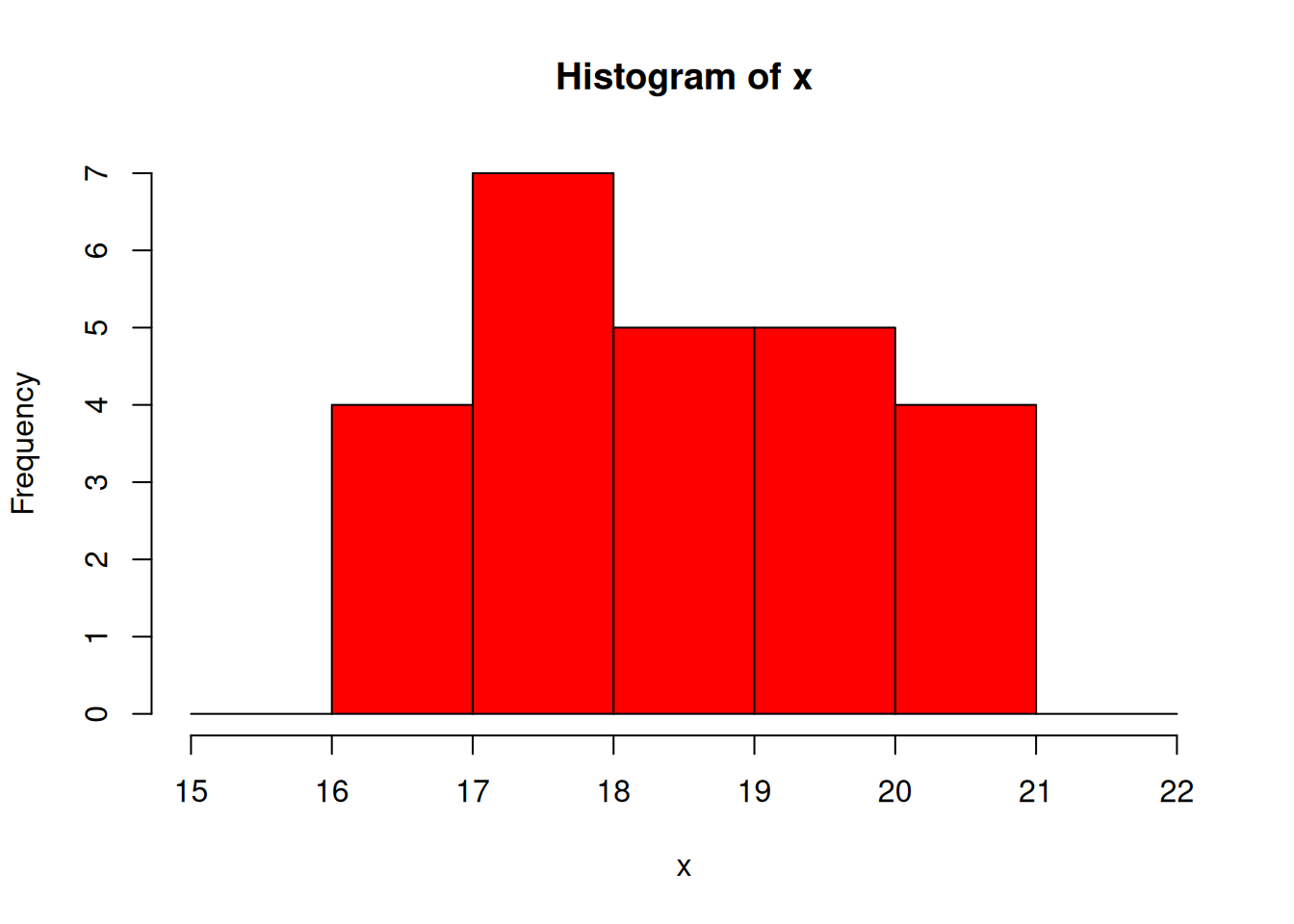

Show the density instead of bin counts:

hist(x, col="skyblue", breaks=15:22, freq=FALSE)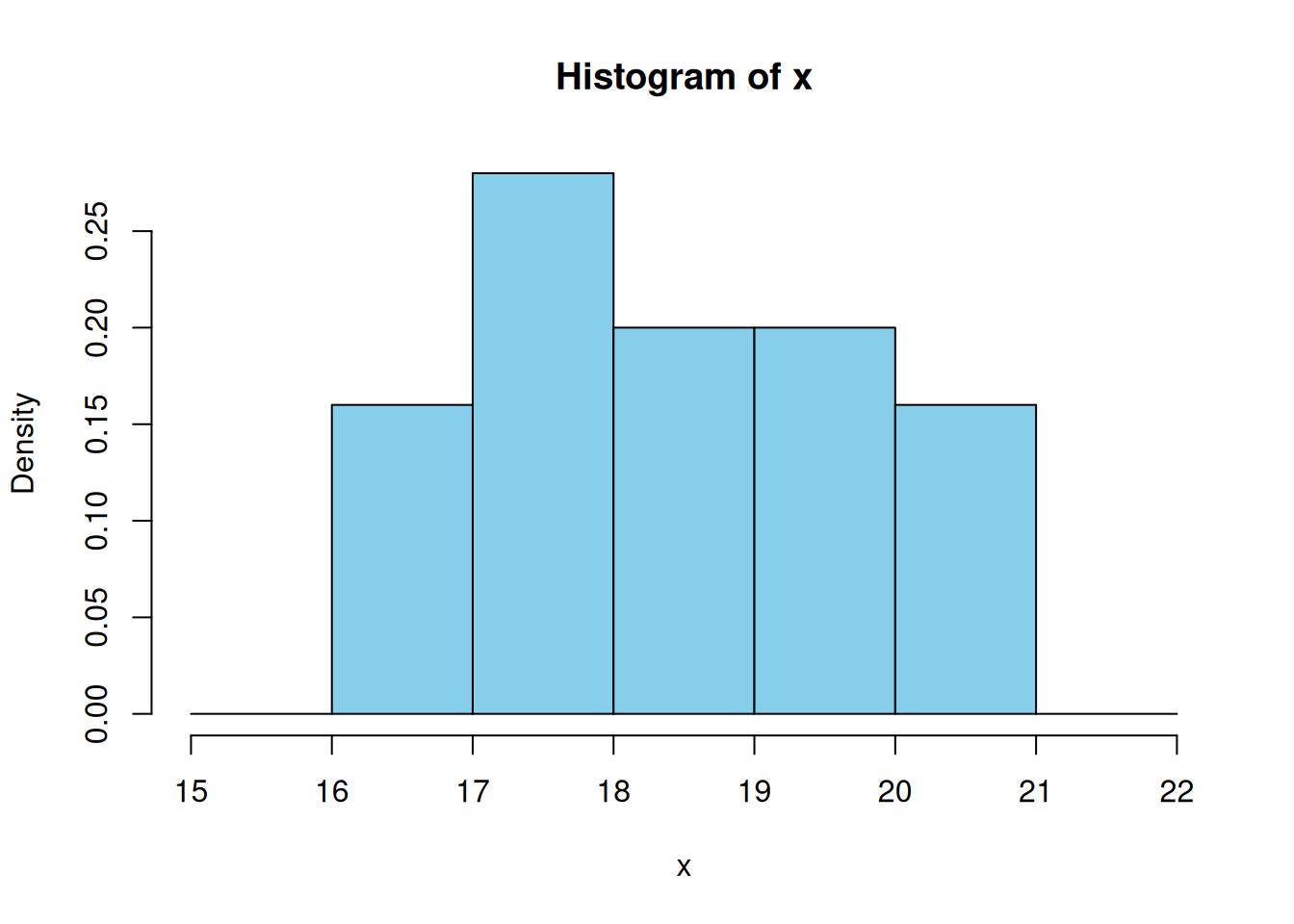

The density values of bars sum up to 1.